In den Medien sehen wir immer wieder Statistiken, doch nicht immer wird richtig argumentiert, manchmal werden die Daten falsch dargestellt oder es werden Aussagen gemacht, die einem genauen Hinsehen und Test nicht standhalten. Beide Beispiele hier können kritisiert werden, das erste, weil eine Kausalität gesehen wird, wo vermutlich keine ist (zumindest kann man sie nicht zeigen, siehe auch Rhetological Fallacies, Information is Beautiful). Im zweiten Beispiel ist der Schluss zwar richtig, aber nur weil es nach etwas aussieht, muss es nicht da sein. Ein Test zeigt dann, die Aussage stimmt.

Für diesen Artikel greife ich einen Blogbeitrag von Philippe Wampfler mit dem Titel Kriminalitätsstatistiken und Rayonverbote auf, der sich mit der Stimmungsmache gegen Asylsuchende befasst. Er bezieht sich dabei auf einen Artikel in der Neuen Luzerner Zeitung. Er schreibt, die Statistik sei problematisch. Er listet auch die Gründe, wieso die Grafik in der Zeitung zumindest nicht perfekt ist. Ich möchte hier nur kurz auf die Statistik eingehen, denn vom einfachen Zahlenanschauen wird man selten schlauer.

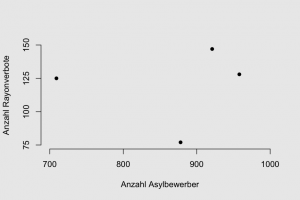
yrs <- 2008:2011 # Jahre 2008 bis 2011
 ab <- c(878, 958, 709, 921) # Anzahl Asylbewerber pro Jahr
 rv <- c(77, 128, 125, 147) # Anzahl Rayonverbote
 rrv <- rv / ab # relative Anzahl Rayonverbote, im Bezug auf Asylbewerber

summary(lm(rv ~ ab)) # erkläre Anzahl Rayonverbote mit Anzahl Asylbewerbern

 summary(lm(rrv ~ ab)) # erläre relative Anzahl Rayonverbote mit Asylbewerbern

 summary(lm(rv ~ yrs)) # erkläre Anzahl Rayonverbote mit den Jahren (je länger je mehr?)

 summary(lm(ab ~ yrs)) # Je länger je mehr Asylbewerber?

Die Ergebnisse sind klar. Kein Erklärungsversuch ist signifikant, also haben weder die Anzahl Asylbewerber noch das Fortschreiten der Jahre einen Effekt auf die absolute Anzahl der Rayonverbote (rv, erstes Modell). Auch wenn ich die Zahlen der Rayonverbote relativ nehme, haben die Zahlen der Asylbewerber keinen Einfluss. Dazu müssen wir aber berücksichtigen, dass die Sample Size, also die Anzahl unserer Werte, ziemlich klein ist. Mit nur vier Werten können wir sehr wahrscheinlich kaum einen Trend erkennen, wenn er da wäre. Aber zumindest lässt sich sagen, dass mit diesen Daten auch keine Trends erkennen lassen, die im Artikel genannt werden.

Ein zweites Beispiel: Die bz Basel schrieb diesen Sonntag, 17 der 25 grösseren Schweizer Städte seien links regiert. Nun denn, schauen wir einmal und machen einen χ²-Test (Chi-Quadrat-Test):

chisq.test(x = cbind(17, 8), p = c(0.303, 0.697))

Kurz zur Erklärung: Die Daten (17, 8) entsprechen den links regierten respektive bürgerlich regierten Städten. Mit dem Argument p wird definiert, was wir erwarten würden, falls es keinen Unterschied gibt und beide politischen Lager so viele Städte regieren, wie man aufgrund ihrer Wählerstärke im Herbst 2011 erwarten würde. Dann hätten die Linken etwas über dreissig Prozent, während die Bürgerlichen auf knapp siebzig Prozent kämen.

Nun denn, das Resultat ist eindeutig:

χ² = 16.8247, df = 1, p = 4.1e-0

Es ist tatsächlich so, dass Linke überproportional viele Städte regieren, der p-Wert liegt bei 0.000041, was um mehrere Grössenordnungen unter der Signifikanzgrenze liegt.

Hier kann man also auch zeigen, dass die Aussage, hier ist etwas spezielles im Gang, wahr ist. Und wir haben gesehen, hier kann mit einem der wohl simpelsten Tests gezeigt werden, dass es stimmt.

Für die Statistik habe ich die geniale freie Software R benützt. Der verwendete Code hier im Artikel (mit Ausnahme der Resultate) kann direkt so in R laufen gelassen werden und er ergibt die gleichen Resultate. Der gesamte Code mit dem Extracode für die Grafik kann auch als R-File heruntergeladen und dann in R ausgeführt werden: R-file-examples.

Foto von mac steve auf Flickr